原文自博客发布平台medium,作者为 Frank Zielen,传送门
质数构成了现代密码学的基础。而其中的原因很简单:直到现在我们还不清楚质数的数学性质规律。然而,通过分解质数,我们发现世界会发生巨大的变化。在这篇文章当中,我会介绍一些关于素数鲜为人知但十分有趣的特性,而且这些特性会改变你对密码学的看法。还有别担心,我会以通俗易懂的方式来介绍给大家的。
刷新认识和找到动机
让我们来回顾一下:质数是指只能被1和它本身整除的整数。例如,5是质数(被1和5整除),但6不是(能够被1,2,3和6整除)。
质数有无数个并且到此为止都没有明确的算法能够准确求得质数。而且,也没有公式去求得第n个质数。即使知道前面的质数也没法通过递归来求得。也没有明确的方法,所以即便不清楚前面的质数,我们也可以计算得出接下来的质数。
正因如此,这使得著名的 RSA 加密如此的安全。它的加密的公钥是通过两个非常大的质数的乘积得出的。这样的话,如果你想导出所需要解密的密钥,“只需要”知道这两个质数的乘积即可。但是,在目前找出这两个质数这需要花费大量的计算时间,所以 RSA 在当前是无法破解的。
但是,如果我们现在发现一条公式来计算质数的话会怎么样呢?我想这会意味着可能产生能够快速破解质数的方法,这对于当前的大多数密码系统来说意味着死刑。但是真的有可能找到这种公式吗?
神奇的欧拉乘积
Leonhard Euler(莱昂哈德 欧拉)是世界上最杰出的数学家之一。在18世纪,他得出了一条今天被称为“欧拉乘积”的公式。在这里,我们把焦点关注在这个发现的一个特殊的例子上吧。提醒一下,即使下一行看起来像是象形文字,也请你不要停止阅读。
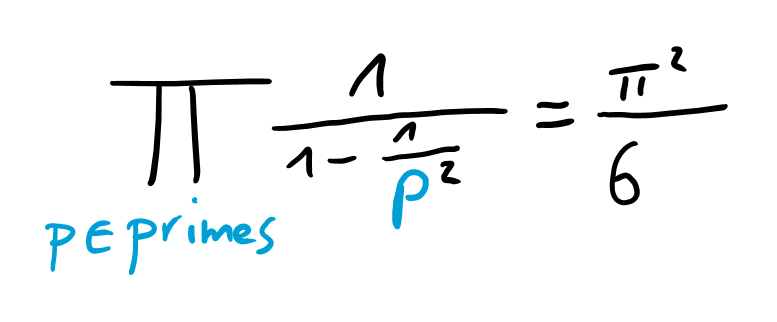
让我们来对此进行翻译:等式左边的符号我们表示为乘积。此外,它也代表所有质数的无穷乘积,即我们需要用所有的质数来替换p并且得到它们的乘积。让我们把这清楚地写在下面。

这表示:如果我们计算以上所有质数的乘积,我们就能够得到一个被预定的结果 pi^2/6。这非常地酷但是看起来不太寻常。那请让我来告诉您当中的原因吧。
破坏性结论
我们知道有无限的质数存在,但是我们并没有接近和有效的表示质数的公式。但有了计算能力,我们可以确定已知的最大质数了。尽管如此,欧拉也证明了,我们没法知道所有的质数,但如果我们根据欧拉乘积将所有质数相乘,将会得到pi^2/6。
恕我直言,这并没有表明到目前为止我们能发现非常多关于质数的知识。如果我们能够在无穷多的质数上计算出欧拉公式,那么我们应该也能通过此导出关于质数的公式。例如,对于一些特殊的质数来说,相近的表达方式是已知的。
这表示我们现在必须加大对数字理论研究的脚步了,以此来发现质数更多的自然规律,并且在这个问题上苦苦研究的人们也会因此感受到快乐和迷惑吧。
结尾
我曾今问过自己这种书呆子一样的问题是否能够吸引到读者。我是一个数论爱好者,但是,这不是我日常的工作所以我会仔细观看大家的评论。如果你想进一步了解有关数论的知识,请告诉我,也许后续我会写一篇相关的文章。